常用图论算法

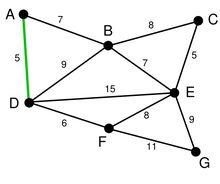
本笔记总结一些常用的图论算法。

参考链接有：

数据结构与算法 - 图论

笔记目录：

最短路径算法
- 无权最短路径 (广度优先算法)
- 有权最短路径 (Dijsktra、Floyd 算法)
最小生成树
- Prim 算法
- Kruskal 算法

最短路径算法

无权最短路径

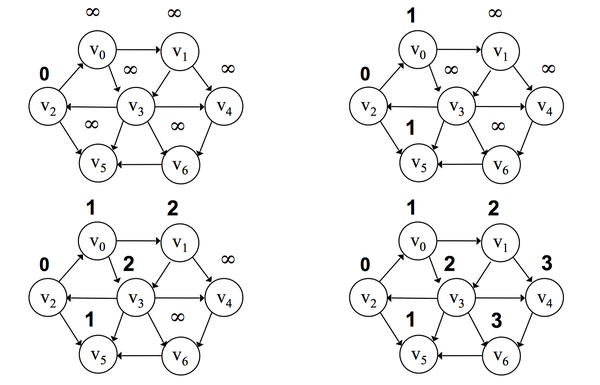
一般使用广度优先算法作为无权的最短路径算法。最短路径算法求的是一个点到其余所有点的最短路径

基本步骤：

将所有点的距离 d 设为无穷大
挑选初始点 s，将 ds 设为 0，将 shortest 设为 0
找到所有距离为 d 为 shortest 的点，查找他们的邻接链表的下一个顶点 w，如果 dw 的值为无穷大，则将 dw 设为 shortest + 1
增加 shortest 的值，重复步骤 3，直到没有顶点的距离值为无穷大

let Node = function() {
    this.isVisited = false;
    this.distance = -1;
    this.next = []; // Array of next nodes
}

function BFS(start) {
    if (start.next.length === 0) {
        return start;
    }
    let queue = [];
    start.distance = 0;
    queue.push(start);
    while (queue.length !== 0) {
        let node = queue.unshift();
        let distance = node.distance;
        node.isVisited = true;
        node.next.forEach(function(node) {
            if (!node.isVisited) {
                node.distance = distance + 1;
                queue.push(node);
            }
        });
    }
    return start;
}

有权最短路径算法

在有权图中，常见的最短路径算法有 Dijkstra 算法 Floyd 算法

Dijkstra 算法

迪杰斯特拉 Dijkstra 算法：Dijkstra 算法适用于权值为正的的图

Dijkstra 算法属于单源算法，即只能求出某点到其它点最短距离，并不能得出任意两点之间的最短距离。该算法类似于边上有权值的最短路径算法，其本质是贪婪算法，贪婪算法一般分阶段求解一个问题，并且在每个阶段都把出现的当做是最好的去处理。

算法步骤：

将所有边初始化为无穷大
选择一个开始的顶点，添加到优先队列中
对于该点的所有邻接顶点进行判断，如果到该点的距离小于原先的值，则将该值进行更新
将该点所有邻接顶点添加到优先队列中
从优先队列中挑选出一个路径值最小的顶点，将其弹出，作为新的顶点，重复步骤 3，4，5
直到所有点都被处理过一次

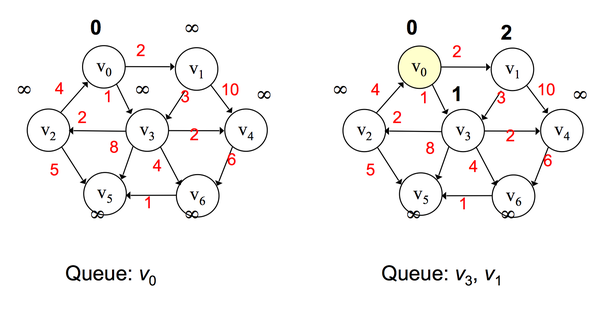
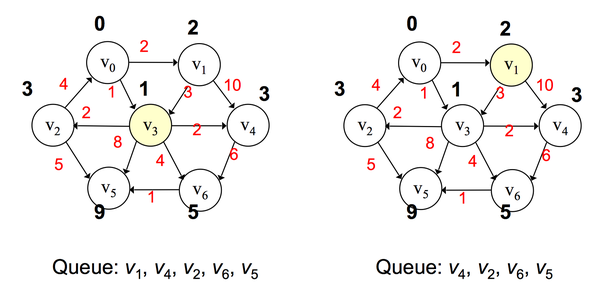
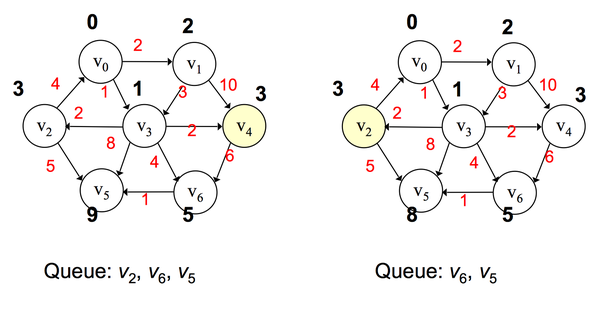
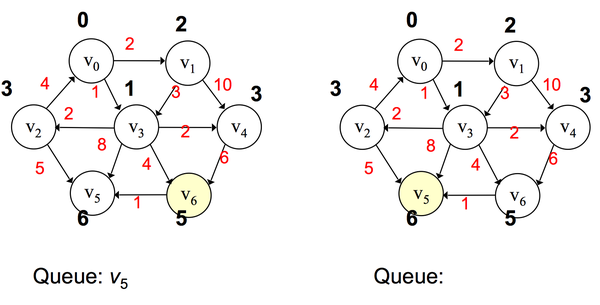
Dijkstra 算法适合于权值为正的情况下，若权值为负则不能使用，因为出现死循环。这时候我们需要计算每个顶点被处理的次数，当某个顶点已经处理过的话，就跳出该循环。

该算法的运行时间依赖对顶点的处理方法，我们必须妖绿顺序扫描顶点以找出最小值的算法。可以将顶点存储在优先级队列中。

如果一个图有负价边，问题在与，一个顶点 u 被声明是 known 的，那个可能从另一个 unknown 的顶点 v 有一条回到 u 的负的路径，在这样的情况下选取从 s 到 v 再回到 u 的路径要比直接从 s 到 u 但不通过 v 更好。

还有一种更简单的例子：假如一张图里有一个总长为负数的环，那么Dijkstra算法有可能会沿着这个环一直绕下去，绕到地老天荒…

let Node = function() {
    this.isVisited = false;
    this.distance = Number.MAX_VALUE;
    this.next = []; // Array of next nodes
    this.link = new Map();  // map of node link, key is node, value is weight
};

function Dijkstra(start) {
    if (start === null) {
        return start;
    } 
    start.distance = 0;
    let queue = [];
    queue.push(start);
    while (queue.length !== 0) {
        let min = Number.MAX_VALUE, minNode;
        for (let i = 0; i < queue.length; i++) {
            if (queue[i].isVisited === false && queue[i].distance < min) {
                minNode = queue[i];
                min = queue[i].distance;
            }
        }
        minNode.isVisited = true;
        minNode.forEach(function(node) {
            let minDis = minNode.distance + minNode.link.get(node);
            node.distance = node.distance < minDis ? node.distance : minDis;
            if (!node.isVisited) {
                queue.push(node);
            }
        });
    }
    return start;
}

Floyd 算法

Floyd 算法可以求出任意两点的最短距离

Floyd 算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点 i 到点 j 的最短路径。

从任意节点 i 到任意节点 j 的最短路径不外乎 2 种可能：

是直接从 i 到 j
是从 i 经过若干个节点 k 到 j

所以，我们假设 Dis(i,j) 为节点 u 到节点 v 的最短路径的距离，对于每一个节点 k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j) 是否成立，如果成立，证明从 i 到 k 再到 j 的路径比 i 直接到 j 的路径短，我们便设置 Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点 k，Dis(i,j) 中记录的便是 i 到 j 的最短路径的距离。

时间复杂度： O(n^3)

for(int k=0; k<n; k++) { 
    for(i=0; i<n; i++) {
         for(j=0; j<n; j++)
             if(A[i][j]>(A[i][k]+A[k][j])) {
                  A[i][j]=A[i][k]+A[k][j];
                  path[i][j]=k;
             } 
    }
}

最小生成树

最小生成树数是由连接图 G 的所有顶点的边构成的树，并且其总价值最低。

Prim 算法

算法思想：找到一个顶点 v 在 known 数组中，另一个顶点 u 在 unknown 数组中，并且权值最小的边，添加到图中。

使用 Prim 算法也需要遍历 known 数组中顶点的所有边，找到权值最小的边，时间复杂度为 O(n*n)

算法步骤：

输入：一个加权连通图，其中顶点集合为 V，边集合为 E
初始化：Vnew = {x}，其中 x 为集合 V 中的任一节点(起始点)，Enew = {} 为空
在集合 E 中选取权值最小的边 <u, v>，其中 u 为集合 Vnew 中的元素，而 v 不在 Vnew 集合当中，并且 v∈V (如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）
将 v 加入集合 Vnew 中，将 <u, v> 边加入集合 Enew 中
重复步骤 3、4 直到 Vnew = V

时间复杂度：O(V^2)